The field of biophysics covers a vast umbrella of topics and subfields. During my graduate career at Rutgers University I delved into several of these subfields in an attempt to understand the workings of living matter. My approach has been primarily through the avenues of complex network science and inference, molecular evolution and population genetics modeling, the study of stochastic processes, and objective function optimization. The following sections overview some of the work I have completed in the last few years on these topics.

Complex Networks

The instances of complex networks in the life sciences are numerous. Examples include protein interaction networks, neural networks, networks of predator-prey interactions, etc. In my own research, I have focused on weighted, undirected networks (i.e. the edge weights $w_{ji} = w_{ij}$ are symmetric between nodes $i$ and $j$), the main contribution being a general Bayesian theoretical formalism for generating estimators of global network properties given only a very small sample of the entire system, $<1\%$. The data acquisition method I have studied for this resarch is random walk sampling: after each network node is sampled, a random neighbor is chosen from the links directly connected to that node as the next sample, and this process is continued until the number of desired samples is attained.

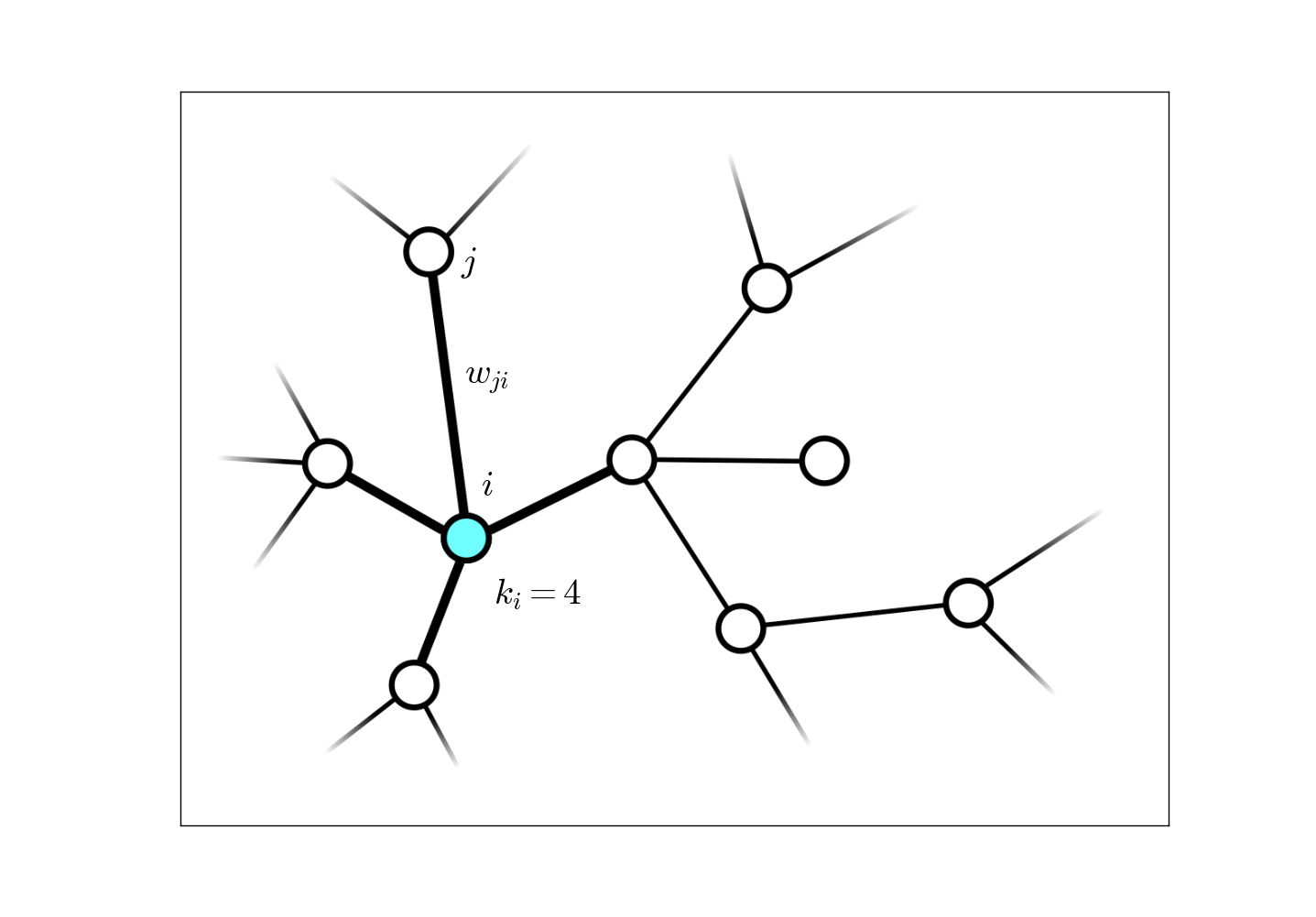
As an example of an estimator generated by our Bayesian formalism, the estimator for the network-wide average connectivity, denoted $\langle k \rangle\equiv \sum_i k_i / N$ for a network with $N$ nodes, is given by

\begin{aligned} \widehat{\langle k \rangle} = \frac{\ell}{\sum_k \mathcal{K}_k / k}, \end{aligned}

when $\ell\ll N$ nodes have been sampled, and $\mathcal{K}_k$ nodes with connectivity $k$ have been visited (this includes repeated visits to the same node.) This formula, derived through this Bayesian formalism, looks very odd when compared to what is typically done when nodes are sampled uniformly,

\begin{aligned} \widehat{\langle k \rangle} = \frac{\sum_k k \mathcal{K}_k}{\ell}, \end{aligned}

and yet proves to be a much better estimator!

This formalism also establishes a rigorous error analysis which yields a high probability range for these estimators. For this particular quantity, this error range falls off as $\sim 1/\sqrt{\ell},$ independent of the network size! This estimator captures the true value long before the diffusive process of the random walk reaches equilibrium. For further detail and other examples of network property estimators that this formalism yields, including one for the full network size, see this paper.

Epidemiology

A clear example of a complex network in the life sciences is the network of geographical regions through which a pathogen might spread. This could be the network of all major cities in the world, with dynamical links representing traffic between each city, or the network of all major airports, etc. Such a model has been developed in this paper where it has been shown that there is a critical value for the node infection probability upon pathogen exposure, $\beta$, which is connected to the average network connectivity by

\begin{aligned} \beta_\text{critical} \propto \langle k \rangle, \end{aligned}

above which there can be a sustained epidemic outbreak in the system. This is a valuable quantity to estimate, and is a prime example of a network property which is rapidly attained when employing random walk sampling instead of uniform sampling.

Although the infection process itself is dynamic as the disease spreads, random walk sampling is indeed applicable given a “rapid-enough” sampling process. This network has been sampled both in this poster and this paper and the fraction of nodes (cities) infected, $\rho(t)$, accurately estimated and tracked as a function of time. This then suggests an alternative method for tracking the course of epidemic diseases, such as the recent Ebola outbreak.

Cancer Research

Although in its early stages, I have begun a project to use the network sampling methodology to determine which groups of genes are responsible for the metabolism of cancerous cells. More to come on this topic in the near future!

Molecular Evolution

Outside the realm of complex network science, much of my graduate career has been spent modeling life processes on both the molecular and population levels. My main objective has been the development of a biophysical model for the computational prediction of genomic features such as the codon usage bias.

Predicting the Codon Usage Bias

The central dogma of biology has triplets of nucleotides called codons translated into amino acids for the production of all proteins. As there are far more codons than amino acids, this translation code is necessarily degenerate with as many as six codons translated into a single amino acid. With the functionality of proteins determined by their amino acid sequences, the choice of synonymous codon should be random or determined solely through mutational rates. However, this is not what is observed in coding sequence data. The unexpected enrichment in the usage of certain synonymous codons is known as the codon bias.

A proposed explanation for this bias is that certain codons are more efficiently translated by the ribosome than others. Efficiency can be characterized as a balance between translation speed and accuracy: a particular codon may be more rapidly translated due to a higher concentration in the tRNA pool, but may also result in more translation errors. These translation errors are the direct result of the Wobble Hypothesis which states that each codon can be recognized by other-than-cognate tRNA species with each mispairing only occuring in the 3’ nucleotide position.

$~$
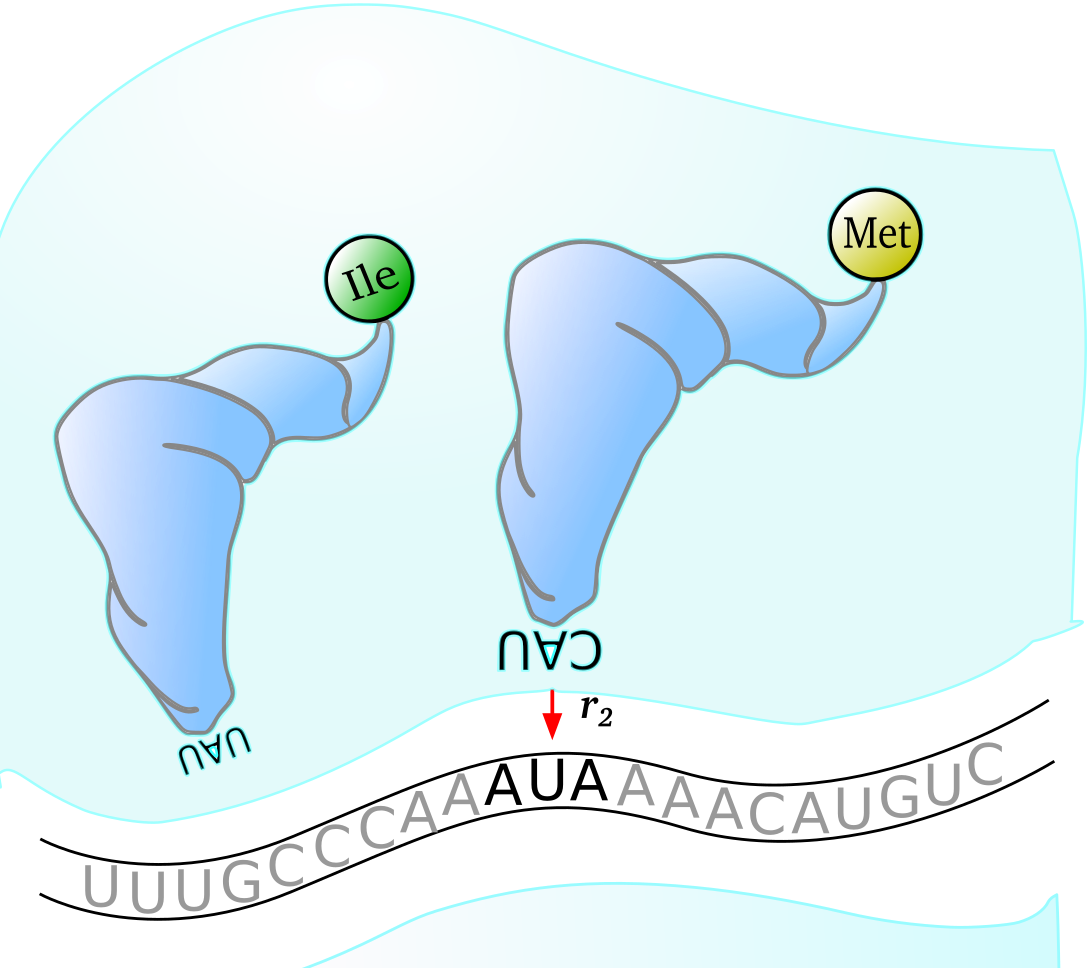
The above image of the mechanics of a ribosome during translation in Escherichia coli shows how wobble pairing can be responsible for an amino acid swap (Isoleucine to Methionine when anticodon CAU pairs with codon AUA) during protein production on a thrA gene transcript. Both of these tRNA species shown are present in E. coli K-12 MG1655 cells and so this mispairing can indeed occur.

For this project the fitness of an organism is modeled as a function of codon translation efficiency. With reasonable biophysical parameters the codon bias is well characterized as a balance between mutation and selection on translation speed and accuracy when the Wobble Hypothesis is included in sufficient detail. Additionally the effects of the topology of the network formed by single-point mutations between codons significantly contribute to the codon bias. For further details on this project see the section on presentations and posters, and this paper.

Objective Function Optimization

Evolutionary biology is ripe with instances of optimized physiology and behaviors. In the field of computer science, many modern optimization algorithms designed to find the extremum of some objective function are based on, or inspired by, natural phenomena. Examples include simulated annealing; guided by the laws of statistical mechanics, and genetic algorithms; structured to mimic evolutionary processes. These algorithms often put faith in some underlying principle. An alternative approach could be to develop a strategy-based algorithm which makes intelligent choices based on the local information of the objective function landscape, and updates its decisions after considering the history of the optimization.

A strategy-based algorithm has been employed in the codon bias project described previously, and a general formulation is in production. Below is an animation of one of the early algorithms learning to rotate a cluster of rigid mass points into the first octant.